
THERMOPHIL Models
THERMOPHILPATh© 2008
In 1999 Jenkins and Roobottom [1] proposed a predictive method for lattice potential energies/enthalpies of ionic solids. They developed an approach to estimate thermochemical radius and close packed single ion volume data for ions for which no salts have yet been prepared, by virtue of the extended database of ion parameters which they provided. The capability of prediction of the molecular (formula unit) volume of new and as yet unprepared materials by combination of single ion volumes can also provide an estimate of the density of that material, considering the fact that effective close-packing ion volumes are additive. Thus the density may be estimated by
[1] 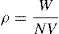
where ρ is the density in kg.m3, W is the molar mass in kg.m-1, N is the Avogadro constant and V is the molecular volume of the salt, in m3 molecule-1 unit, which is assumed as the linear sum of the volumes of cation (V+) and anion (V-).
This method was recently extended to ionic liquids by Ye and Shreeve [2] with success but limited to the estimation of densities at atmospheric pressure and room temperature. Based on this approach we proposed an extension of the Ye and Shreeve group contribution method for the estimation of ionic liquids densities in a wide range of temperatures (273.15 - 393.15 K) and pressures (0.10 - 100 MPa).
The isothermal compressibility, kT, is defined as
[2] 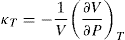
and the isobaric expansivity, αT is defined as
[3] 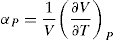
Combining the pressure and temperature dependence of the molecular volume and integrating this equation the dependency of the molecular volume in pressure and temperature is obtained as
[4] V=V0e(x+αpT + kTP)
where V0 is constant and x is equal to -(αPT0 + kTP0).
Expanding Eq. (4) in a Taylor series and retaining just the first members of the series Eq. (4) is simplified on
[5] V=V0(a+bT+cP)
where V0 is the molecular volume at the reference temperature (T0) and pressure (P0) in m3 molecule-1, whereas the coefficients a are (1 + x), b is αP and c is κT. The b and c constants will be taken as ionic liquid independent as the αP and kT for most of the ionic liquids investigated seem to have a fairly constant value.
Using Eq. (5), it is possible to obtain a pressure and temperature dependent version of Eq. (1):
[6] 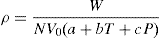
The coefficients a, b and c can be estimated by fitting Eq. (6) to experimental data. Here they were estimated by correlating the experimental densities of nine ILs previously measured by us [3] and [4] covering the density range (986.7 ± 1547.1 kg.m3), temperature range (293.15±393.15 K) and pressure range (0.10 ± 30.00 MPa). A total amount of circa 800 density data points were used. The values of coefficient a, b and c obtained are 8.005x10-1 ± 2.333x10-4, 6.652x10-4 ± 6.907x10-7 K1 and -5.919x10-4 ± 2.410x10-6 MPa-1, respectively, at 95% level of confidence.

Surface Tension
Experimental data for surface tensions of ILs is very scarce ad essentially restricted to imidazolium based ILs. Using surface tension data of ILs measured in our laboratory along with a database obtained from the literature, a correlation was developed for the surface tensions of ILs [5] showing that it is possible to use parachors to obtain good predictions for surface tensions of ionic liquids.
The surface tensions of ionic liqudis can be obtained using the following equation,
[7] γ=(Pch.ρ/Mw)4
where Pch is the parachor which is calculated from Knotts et al. [6] parachor QSPR correlation using the parameter table estimated from the second training set containing experimental surface tension values with an uncertainty less than 1 % and ρ is the density obtained using equation 6, of imidazolium based ILs display a good agreement with the corresponding experimental surface tensions (γexp): γcalc=(0.987 ± 0.004)γexp.
For the 361 data points of 38 imidazolium based ILs studied, the overall MPD is 5.75 %, and a maximum deviation inferior to 16 % observed.
the predictive capability of eq. 7 for IL surface tension was further checked below through its potential to correlate the speed of sound of ILs through the Auerbach's relation.

Speed of Sound- Auerbach's relation
Experimental data for speed of sound of ILs is scarce and limited to imidazolium based ILs. The speed of sound (u) in m.s-1 units can be estimated using the surface tension (γ) in N.m-1 units and density (ρ) in Kg.m-3 units, through the theoretical Auerbach's relation [7].
[8] u=(γ/6.33x10-10.ρ)2/3
To examine the functional dependence of u and γ/ρ, a double logarithmic plot was drawn using speed of sound data from literature, density and surface tension obtained using eqs. 6 and 7 respectively, and the resulting linear correlations was
[9] log uexp=(0.6199 ± 0.0092).log(γ/ρ)+(5.9447 ± 0.0414)
with a correlation coefficient R2=0.9717 at 95 % confidence level.
Through eq. 8 directly is not capable to predict sound velocities of ILs, a modified version of it, following the approach of Oswal et al. [8,9], could be used to correlate the speed of sound of ILs [10].
The experimental speed of sound (uexp) of imidazolium based ILs displays a good agreement with corresponding calculated speed of sound (ucalc) using eq. 9 where uexp=(0.9952 ± 0.0022)ucalc. For the 133 data points of 14 imidazolium based ILs, the overall MPD is 1.96 % with maximum deviation inferior to 5 %.

Viscosities - Vogel-Tammann-Fulcher equation
A correlation based on the Vogel-Tammann-Fulcher equation was proposed [11]
[10] 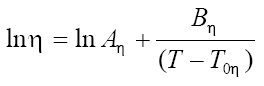
where η is the viscosity in Pa.s units, T is the temperature in K and Aη, Bη and T0η are adjustable parameters. The ratio of parameters Bη, T0η and Bη/T0η is also known as Angell strength parameter. It was found that the optimum value of T0η is 165.06 K. Aη and Bη can be obtain by group contribution method according to
[11] 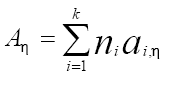
[12] 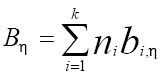
where ni is the number of groups of type i and k is the total number of different groups in the molecule, and the parameters ai,η and bi,η here estimated are presented in ref. [11]. Close to 500 data points of 25 ILs based on imidazolium, pyridinium and pyrrolidinium cations with different anions, covering wide ranges of temperatures, 293.15-393.15 K and viscosity, 0.004-1.065 Pa.s, were used in the study.
The calculated viscosity (ηcalc) of the Ils studied displayed a good agreement with the corresponding experimental viscosity (ηexp), where ln ηcalc=(0.9647 ± 0.0043).ln ηexp (R2=0.9907 at 95 % level of confidence). For 482 data points of 25 ILs available in literature, the overall MPD is 7.50 % with maximum deviation inferior to 23 %. Rejection of doubtful experimental data was not possible due to the limited amount of experimental data currently available and the large discrepancies in experimental viscosity values reported in literature among authors, which may be due to impurities like water and halogen ions present in ILs samples, or the experimental method adopted.
The predictive capability of the developed group contribution method for ILs viscosity was further checked by its potential to correlate with equivalent conductivity and the self-diffusion coefficient using fractional forms of Walden rule [12] and Stokes-Einstein relation [13], respectively.

References
[1] H.D.B. Jenkins and H.K. Roobottom, Inorg. Chem. 38 (1999), pp. 3609-3620.
[2] C. Ye and J.M. Shreeve, J. Phys. Chem. A 111 (2007), pp. 1456-1461.
[3] R.L. Gardas, M.G. Freire, P.J. Carvalho, I.M. Marrucho, I.M.A. Fonseca, A.G.M. Ferreira and J.A.P. Coutinho, J. Chem. Eng. Data 52 (2007), pp. 80-88.
[4] R.L. Gardas, M.G. Freire, P.J. Carvalho, I.M. Marrucho, I.M.A. Fonseca, A.G.M. Ferreira and J.A.P. Coutinho, J. Chem. Eng. Data 52 (2007), pp. 1881-1888.
[5] R.L. Gardas and J.A.P. Coutinho, Fluid Phase Equilib. 265 (2008), pp. 57-65.
[6] T.A. Knotts, W.V. Wilding, J.L. Oscarson, R.L. Rowley, J. chem. Eng. Data 46 (2001) pp. 1007-1012.
[7] R. Auerbach Oberfla chenspannung und Schallgeschwindigkeit. Experientia 4 (1948) pp. 473-474
[8] S.L. Oswal, P. Oswal, P.S. Modi, J.P. Dave, R.L. Gardas, Thermochim. Acta 410 (2004) pp. 1-14
[9] S.L. Oswal, P. Oswal, S.G. Patel, R.G. Shinde, Fluid Phase Equilib. 216 (2004) pp. 33-45
[10] R.L. Gardas and J.A.P. Coutinho, Fluid Phase Equilib. 267 (2008), pp. 182-186.
[11] R.L. Gardas and J.A.P. Coutinho, AIChe J. 55 (2009), pp. 1274-1290.
[12] P. Walden, Z. Phys. Chem. 55 (1906), pp. 207-249.
[13] J.O.M. Bockris and G.W. Hooper, Discuss. Faraday Soc. 32 (1961), pp. 218-236.


